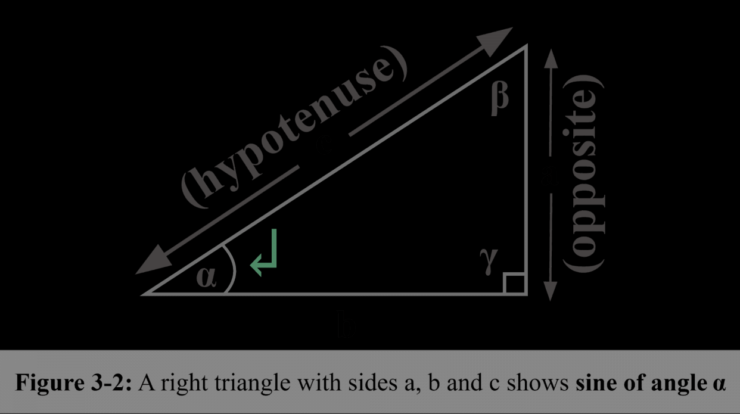
Sine definition, a cornerstone of trigonometry, embarks us on a journey into the fascinating realm of periodic functions, revealing their applications across diverse fields.

Delving into the sine function’s properties, we unravel its periodicity, amplitude, and intricate relationship with its trigonometric counterpart, cosine.

Define Sine Function

The sine function is a trigonometric function that describes the vertical displacement of a point on a unit circle as the angle from the horizontal axis increases. It is a periodic function with a period of 2π.

The mathematical formula for calculating the sine of an angle θ is:

sin(θ) = y/r

where y is the vertical coordinate of the point on the unit circle and r is the radius of the circle.

Properties of Sine Function

The sine function has several important properties:

• Periodicity: The sine function repeats itself every 2π radians.
• Amplitude: The amplitude of the sine function is 1, which means that the maximum and minimum values of the function are -1 and 1, respectively.
• Relationship with Cosine: The sine function is related to the cosine function by the following identity:

sin(θ) = cos(π/2

θ)

Applications of Sine Function, Sine definition

The sine function has numerous applications in real-world situations, including:

• Physics: The sine function is used to model the motion of objects in periodic motion, such as pendulums and springs.
• Engineering: The sine function is used to analyze the strength of structures and to design bridges and buildings.
• Music: The sine function is used to create sound waves, which are the basis of music.

Graphing Sine Function

The graph of the sine function is a wave that oscillates between -1 and 1. The key features of the graph include:

• Intercepts: The sine function intercepts the y-axis at (0, 0) and the x-axis at (π, 0) and (2π, 0).
• Asymptotes: The sine function has no asymptotes.

Inverse Sine Function

The inverse sine function, also known as the arcsine function, is the function that undoes the sine function. The formula for calculating the inverse sine of a number x is:

sin^-1(x) = θ

where θ is the angle whose sine is x.

The inverse sine function has a range of [-π/2, π/2] and a domain of [-1, 1].

Final Wrap-Up

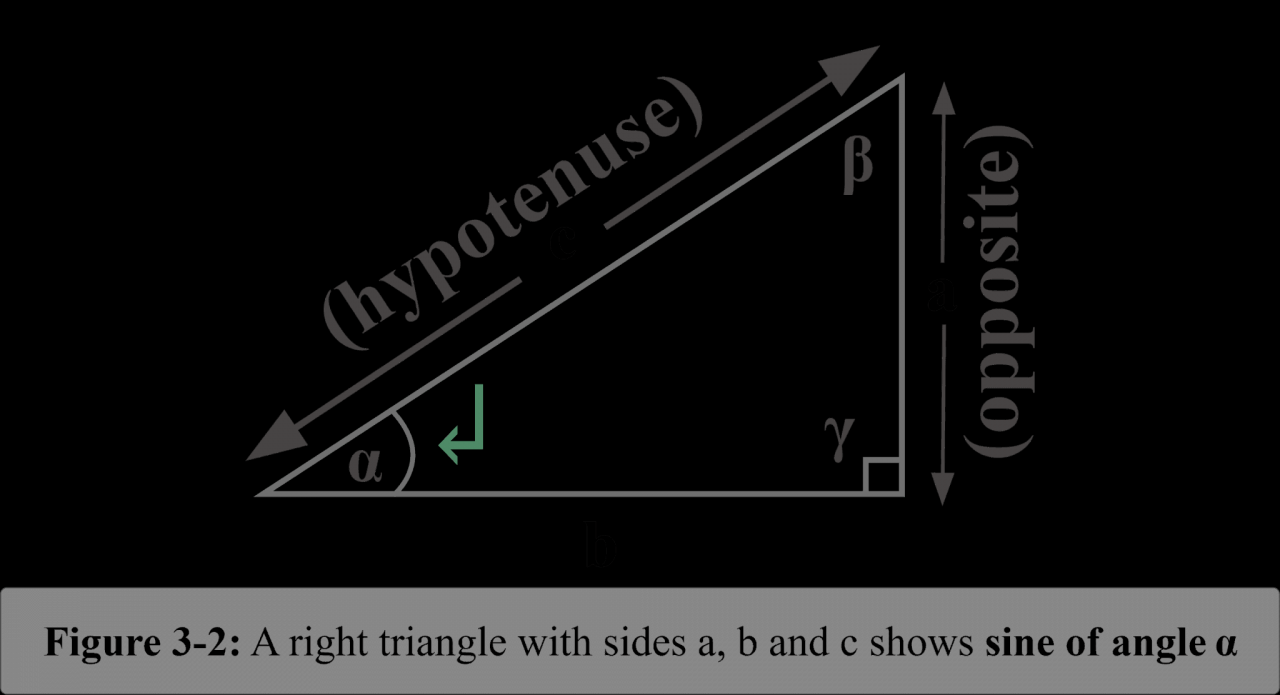
From the rhythmic oscillations of sound waves to the graceful trajectories of celestial bodies, the sine function permeates our world, serving as a fundamental tool in fields as diverse as physics, engineering, and music.

FAQ Summary: Sine Definition

What is the mathematical formula for calculating sine?

Sine(angle) = Opposite side / Hypotenuse

How is the sine function used in real-world applications?

Sine is used in fields such as acoustics, engineering, and astronomy to model periodic phenomena like sound waves, vibrations, and planetary orbits.

What is the relationship between sine and inverse sine functions?

The inverse sine function, denoted as arcsine, is the inverse of the sine function. It determines the angle whose sine value is a given number.